Answer:
a. P(X = 3) = 0.145736
b. P(5≤X≤9) = 0.5462
c. P(5<X<10) = 0.3332
d. P(X≥6) = 0.3393
e. P(X<5) = 0.4477
f. Mean = 4.8, Variance = 3.264
Explanation:
Given - The same survey database cited in exercise 4.3.1 (A-5) shows
that 32 percent of U.S. adults indicated that they have been
tested for HIV at some point in their life. Consider a simple
random sample of 15 adults selected at a time. Let X be the
number of adults who have been tested for HIV in the sample.
To find - For the following, find the numerical answer and describe
the answer in words:
a. Three
b. Between five and nine, inclusive
c. More than five, but less than 10
d. Six or more
e. Less than five
f. Find the mean and the variance of the number of people
tested for HIV in samples of size 15.
Proof -
Given that , n = 15, p = 32% = 0.32
Now,
a.
P(X = 3) = binomial distribution (3, 15, 0.32, 0)
=
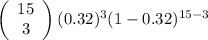
= 455(0.032768)(0.009774)
= 0.145736
⇒P(X = 3) = 0.145736
b.
P(5≤X≤9) = P(X = 5) + P(X = 6) + P(X = 7) + P(X = 8) + P(X = 9)
=
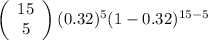 +
+
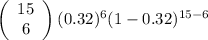 +
+
 +
+
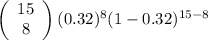 +
+
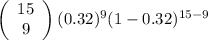
= 0.213 + 0.1671 + 0.1011 + 0.0476 + 0.0174
= 0.5462
⇒P(5≤X≤9) = 0.5462
c.
P(5<X<10) = + P(X = 6) + P(X = 7) + P(X = 8) + P(X = 9)
=
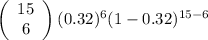 +
+
 +
+
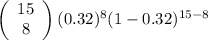 +
+
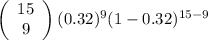
= 0.1671 + 0.1011 + 0.0476 + 0.0174
= 0.3332
⇒P(5<X<10) = 0.3332
d.
P(X≥6) = 1 - P(X < 6)
= 1 - P(X ≤ 5)
= 1 - binomial(5, 15, 0.32, 1)
= 1 - 0.6607
= 0.3393
⇒P(X≥6) = 0.3393
e.
P(X<5) = P(X≤4)
= binomial (4, 15, 0.32, 1)
= 0.4477
⇒P(X<5) = 0.4477
f.
Mean = np
= 15(0.32)
= 4.8
⇒Mean = 4.8
Variance = np(1-p)
= 15(0.32)(1 - 0.32)
= 4.8(0.68)
= 3.264
⇒Variance = 3.264