Answer:
The P-value for this test is 0.0023.
Explanation:
The null hypothesis is:
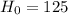
The alternate hypotesis is:

The test statistic is:
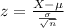
In which X is the sample mean,
 is the value tested at the null hypothesis,
is the value tested at the null hypothesis,
 is the standard deviation and n is the size of the sample.
is the standard deviation and n is the size of the sample.
Previous experience indicates that the standard deviation of tensile strength is 2 psi.
This means that
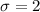
A random sample of eight fiber specimens is selected, and the average tensile strength is found to be 127 psi.
This means, respectively, that
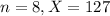
Test the hypothesis that the mean tensile strength equals 125 psi versus the alternative that the mean exceeds 125 psi.
This means that
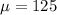
What is the P-value for this test
First we find the test statistic. So
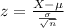
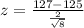
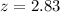
The pvalue is 1 subtracted by the pvalue of Z = 2.83.
Looking at the z-table, we have that:
Z = 2.83 has a pvalue of 0.9977
1 - 0.9977 = 0.0023
The P-value for this test is 0.0023.