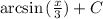Question

Evaluate the following integral using trigonometric substitution

Integral underroot dx/ 9-x^2

Answer 1

The result of the integral is:

`\arcsin{((x)/(3))} + C`

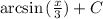
Explanation:

We are given the following integral:

`\int (dx)/(√(9-x^2))`

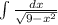
Trigonometric substitution:

We have the term in the following format:
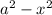`a^2 - x^2`, in which a = 3.

In this case, the substitution is given by:

`x = asin(\theta)`

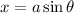
So

`dx = acos(\theta)d\theta`

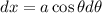
In this question:

`a = 3`

`x = 3sin(\theta)`

`dx = 3cos(\theta)d\theta`

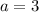
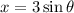
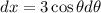
So

`\int (3cos(\theta)d\theta)/(√(9-(3sin(\theta))^2)) = \int \frac{3cos(\theta)d\theta}{\sqrt{9 - 9\sin^(2){\theta}}} = \int \frac{3cos(\theta)d\theta}{\sqrt{9(1 - \sin^(\theta))}}`

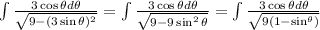
We have the following trigonometric identity:

`\sin^(2){\theta} + \cos^(2){\theta} = 1`

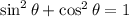
So

`1 - \sin^(2){\theta} = \cos^(2){\theta}`

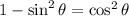
Replacing into the integral:

`\int \frac{3cos(\theta)d\theta}{\sqrt{9(1 - \sin^(2){\theta})}} = \int{\frac{3cos(\theta)d\theta}{\sqrt{9\cos^(2){\theta}}} = \int (3cos(\theta)d\theta)/(3cos(\theta)) = \int d\theta = \theta + C`

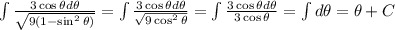
Coming back to x:

We have that:

`x = 3sin(\theta)`

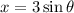
So

`sin(\theta) = (x)/(3)`

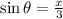
Applying the arcsine(inverse sine) function to both sides, we get that:

`\theta = \arcsin{((x)/(3))}`

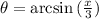
The result of the integral is:

`\arcsin{((x)/(3))} + C`