Answer:
Explanation:
To find the slope of the tangent at a point we will find the derivative of equation at that point.
a). y = x² - 10x
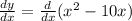
y' = 2x - 10
At (x = 2),
y' = 2(2) - 10
y' = 4 - 10
y' = -6
From the given equation,
y = 2² - 10
y = -6
Therefore, y-coordinate of the point is y = -6
Equation of the tangent at (2, -6) having slope = -6
y - 2 = -6(x - 2)
y - 2 = -6x + 12
y = -6x + 14
b). y =
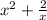
At x =

y =
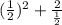
y =
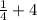
y =
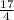
Now we have to find the equation of a tangent at
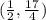
y' = 2x -
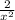
At x =

y' =

y' = 1 - 8
y' = -7
Therefore, equation of the tangent at
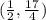 will be,
will be,
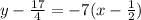
y = -7x +
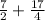
y = -7x +
