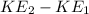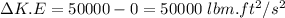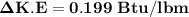Question

Initially, 1 lbm of water is at rest at 14.7 psia and 70 F. The water then undergoes a process where the final state is 30 psia and 700 F with a velocity of 100 ft/s and an elevation of 100 ft above the starting location. Determine the increases in internal energy, potential energy, and kinetic energy of the water in Btu/lbm. Compare the increases in potential energy and kinetic energy individually to the change in the internal energy.

Answer 1

Step-by-step explanation:

`\text{From the information given:}`

`\text{The mass (m) = 1 lbm}`

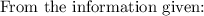
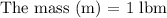
Suppose: g = 32.2 ft/s²

At the inlet conditions:

`\text{mass (m) = 1 \ lbm water} \\ \\ P_1 = 14.7 \ psia \\ \\ T_1 = 70 F \\ \\ z_1 = 0 \ ft`

At the outlet conditions:

`P_2 = 30 \ psia \\ \\ T_2 = 700\ F \\ \\ v_2 =100 \ ft/s\\ \\ z_2 = 100 \ ft`

`\text{Using the information obtained from saturated water table at P1 = 14.7 \ psia \ and \ T1 = 70 F }`

`u_1 =u_f = 38.09 \ Btu/lbm`

`\text{Applying informations from superheated water vapor table:}`

`P_2 = 30 \ psia \ and \ T_2 = 700 \ F \\ \\ u_ = 1256.9 \ kJ/kg`

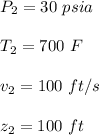
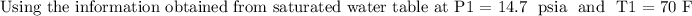
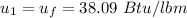
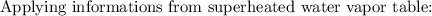
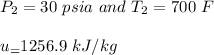
The change in the internal energy is:

`\Delta U = U_2 -U_1 \\ \\ \Delta U = 1256.9 -38.09 \\ \\ \Delta U = 1218.81 \ Btu/lbm`

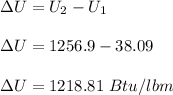
For potential energy (P.E):

Initial P.E = mgz

P.E = 1 × 32.2 × 0 = 0 ft²/s²

Final P.E = mgz

P.E = 1 × 32.2 × 100 = 3220 ft²/s²

The change in the potential energy = PE₂ - PE₁

ΔPE = (3220 - 0) ft²/s²

ΔPE = 3220 ft²/s²

ΔPE = (3220 × 3.9941 × 10⁻⁵) Btu/lbm

ΔPE =0.12861 Btu/lbm

Initial Kinetic energy (K.E)

`KE_1 = (1)/(2)mV_1`

`KE_1 = (1)/(2)(1)(0) = 0 \ lbm \ ft^2/s^2`

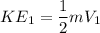
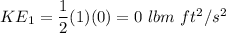
FInal K.E

`KE_2= (1)/(2)mV_2`

`KE_2= (1)/(2)(1)(100)^2_2 = 50000 \ lbm \ ft^2/s^2`

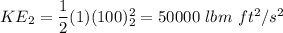
Change in K.E
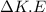`\Delta K.E` =
`KE_2-KE_1`

`\Delta K.E = 50000 -0 = 50000 \ lbm.ft^2/s^2`

`\mathbf{\Delta K.E = 0.199 \ Btu/lbm}`