Question

Cystic fibrosis (CF) is a hereditary lung disorder that often results in death. It can be inherited only if both parents are carriers of an abnormal gene. In 1989, the CF gene that is abnormal in carriers of cystic fibrosis was identified. The probability that a randomly chosen person of European ancestry carries an abnormal CF gene is 1/25. (The probability is less in other ethnic groups.) The CF20m test detects most, but not all, harmful mutations of the CF gene. The test is positive for 90% of people who are carriers. It is never positive for people who are not carriers.

Required:
Compute the probability that a randomly chosen person of European ancestry does not carry an abnormal CF gene given that he /she tested negative.

Answer 1

0.9959 = 99.59% probability that a randomly chosen person of European ancestry does not carry an abnormal CF gene given that he /she tested negative.

Explanation:

Conditional Probability

We use the conditional probability formula to solve this question. It is

`P(B|A) = (P(A \cap B))/(P(A))`

In which

P(B|A) is the probability of event B happening, given that A happened.

`P(A \cap B)` is the probability of both A and B happening.

P(A) is the probability of A happening.

In this question:

Event A: Tested negative

Event B: Does not carry an abdornal CF gene.

Probability of a negative test:

10% of 1/25 = 0.04 = 4%

100% of 100 - 4 = 96%. So

`P(A) = 0.1*0.04 + 1*0.96 = 0.964`

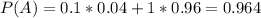
Negative test and not carrying an abdornal gene:

100% of 96%. So

`P(A \cap B) = 1*0.96 = 0.96`

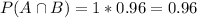
Compute the probability that a randomly chosen person of European ancestry does not carry an abnormal CF gene given that he /she tested negative.

`P(B|A) = (P(A \cap B))/(P(A)) = (0.96)/(0.964) = 0.9959`

0.9959 = 99.59% probability that a randomly chosen person of European ancestry does not carry an abnormal CF gene given that he /she tested negative.