Question

A recent study from the University of Virginia looked at the effectiveness of an online sleep therapy program in treating insomnia. They took 45 random adults who suffered from insomnia. 22 of them were randomly selected to participate in the therapy program while the remaining 23 served as a control group. They scored each individual using an Insomnia Severity Index, and hoped to prove that the participants in the program would have a lower score. For the 22 subjects who participated in the program, the average score was 6.59, with a standard deviation of 4.10. For the 23 subjects in the control group, the average score was 15.50, with a standard deviation of 5.34.

1. Calculate the 99% confidence interval for the difference in averages. What do you conclude?
2. What are some possible issues with your calculation in the previous part?

Answer 1

1. The 99% confidence interval for the difference in average is -6.47377 < μ₁ - μ₂ < -11.34623

2. The possible issues in the calculations includes;

a. The confidence level used in the confidence interval can influence the result of the confidence interval observed

b. The sample size is small

Explanation:

1. The number of adults with insomnia in the sample = 45

The number of adults that participated in the therapy, n₁ = 22

The number of candidates that served as control group, n₂ = 23

The average score for the for the 22 participants of the program,
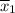`\overline x_1` = 6.59

The standard deviation for the 22 participants of the program, s₁ = 4.10

The average score for the for the 23 subjects in the control group,
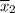`\overline x_2` = 15.50

The standard deviation for the 23 subjects in the control group, s₂ = 5.34

The confidence interval for unknown standard deviation, σ, is given by the following expression;

`\left (\bar{x}_(1)- \bar{x}_(2) \right )\pm t_(\alpha /2)\sqrt{(s_(1)^(2))/(n_(1))+(s_(2)^(2))/(n_(2))}`

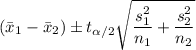
α = 1 - 0.99 = 0.01

α/2 = 0.005

The degrees of freedom, df = 22 - 1 = 21

`t_(\alpha /2)` =
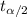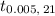`t_(0.005, \, 21)` = 1.721

Therefore, we have;

`\left (6.59- 15.5 \right )\pm1.721 \cdot \sqrt{(4.10^(2))/(22)+(5.34^(2))/(23)}`

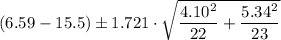
The 99% confidence interval for the difference in average is therefore given as follows;

-6.47377 < μ₁ - μ₂ < -11.34623

Therefore, there is considerable evidence that the participants in the survey had lower average score than the subjects in the control group

2. The possible issues in the calculations are;

a. The confidence level used in the confidence interval can influence the result of the confidence interval observed

b. The sample size is small