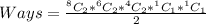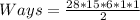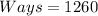Question

In how many ways can 8 different dolls be packed in 5 identical gift boxes such that no box is empty if any of the boxes hold all of the toys?

Answer 1

1260 ways

Explanation:

Given

`Dolls = 8`

`Boxes = 5`

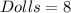
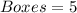
From the question, we understand that: the boxes are identical; however, the dolls are different.

Since no box can be empty, the following scenario exists:

2, 2, 2, 1, 1

This means that 3 of the 5 boxes will hold 2 dolls each while the other 2 will hold 1 doll each.

So, the number of selection is as follows:

2 of the 8 dolls will be selected in 8C2 ways

2 of the remaining 6 dolls will be selected in 6C2 ways

2 of the remaining 4 dolls will be selected in 4C2 ways

1 of the remaining 2 will be selected in 1C1 ways

1 of the remaining 1 will be selected in 1C1 ways

`Expression: ^8C_2 * ^6C_2 * ^4C_2 * ^1C_1 * ^1C_1`

Since the boxes are identical, we have to divide the above expression by 2 to get the number of ways:

`Ways = (^8C_2 * ^6C_2 * ^4C_2 * ^1C_1 * ^1C_1)/(2)`

`Ways = (28 * 15* 6* 1 * 1)/(2)`

`Ways = (2520)/(2)`

`Ways = 1260`