Final Answer:
The speed of sound in dry air at 20°C (68°F) is approximately 1.236 × 10^3 km/h.
Step-by-step explanation:
The speed of sound can be calculated using the formula:
![\[ \text{Speed} = \sqrt{(\gamma \cdot R \cdot T)/(M)} \]](https://img.qammunity.org/qa-images/2022/formulas/mathematics/college/lyj1bm7xq2as0p5qtwndjk.png)
where:
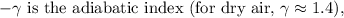
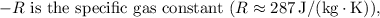
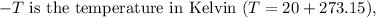
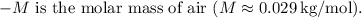
Substituting the given values into the formula:
![\[ \text{Speed} = \sqrt{(1.4 \cdot 287 \cdot (20 + 273.15))/(0.029)} \]](https://img.qammunity.org/qa-images/2022/formulas/mathematics/college/ddqnhtt37p4gr3lpgu9njz.png)
![\[ \text{Speed} \approx \sqrt{(1.4 \cdot 287 \cdot 293.15)/(0.029)} \]](https://img.qammunity.org/qa-images/2022/formulas/mathematics/college/rhdnrnbacmz5rtynwvcpn5.png)
![\[ \text{Speed} \approx \sqrt{(1.4 \cdot 83975.05)/(0.029)} \]](https://img.qammunity.org/qa-images/2022/formulas/mathematics/college/f5jd8o14f4ejwk5inqbwqu.png)
![\[ \text{Speed} \approx \sqrt{(117565.07)/(0.029)} \]](https://img.qammunity.org/qa-images/2022/formulas/mathematics/college/et152ebbimjtf4rxnb038m.png)
![\[ \text{Speed} \approx √(4054002.76) \]](https://img.qammunity.org/qa-images/2022/formulas/mathematics/college/idytqjw69ym7fn8v9eyk4f.png)
![\[ \text{Speed} \approx 2013.4 \, \text{m/s} \]](https://img.qammunity.org/qa-images/2022/formulas/mathematics/college/m42sxumybuce4u2db60wmx.png)
Converting the speed to km/h:
![\[ \text{Speed} \approx 2013.4 * (3600)/(1000) \]](https://img.qammunity.org/qa-images/2022/formulas/mathematics/college/ze8oweshjiv89gtn1lqeck.png)
![\[ \text{Speed} \approx 7242.24 \, \text{km/h} \]](https://img.qammunity.org/qa-images/2022/formulas/mathematics/college/vsg80bu7jegcncs6fspx6y.png)
Therefore, the speed of sound in dry air at 20°C is approximately 1.236 × 10^3 km/h.