Answer:
B) Both functions have a y-intercept of -2.
Explanation:
Hi there!
A) Both functions are always increasing.
⇒ False
Let's first take a look at the given equation,
 . This is a linear equation, and it is organized in slope-intercept form:
. This is a linear equation, and it is organized in slope-intercept form:
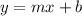 . m is the slope and b is the y-intercept. When m is positive, it is always increasing.
. m is the slope and b is the y-intercept. When m is positive, it is always increasing.
In
 , 3 is m, and because it's positive, this line is always increasing on a graph.
, 3 is m, and because it's positive, this line is always increasing on a graph.
However, when we take a look at the given graph, this isn't the case. It is decreasing for values of x below 0 (on the left side of the y-axis).
B) Both functions have a y-intercept of -2.
⇒ True
In the given equation
 , this is true. -2 is the y-intercept.
, this is true. -2 is the y-intercept.
On the given graph, we can see that the graph intercepts the y-axis at -2, so this is also true for the graph.
C) Both functions are symmetric about the y-axis.
⇒ False
The given graph is symmetric about the y-axis, but the line is not. Any line that would be symmetric about the y-axis would be in the form
 , which isn't the case here with
, which isn't the case here with
 .
.
 has a slope.
has a slope.
D) Both functions are linear relationships.
⇒ False
Sure,
 is a linear equation, making it a line, but not the given graph. The graph does not resemble a straight line, so it is not a linear relationship.
is a linear equation, making it a line, but not the given graph. The graph does not resemble a straight line, so it is not a linear relationship.
I hope this helps!