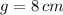Question

ITS AN ANGLE QUESTION PLS HELP

Answer 1

The values of
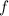`f` and
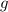`g` are, respectively:

`f = 6\,cm`,
`g = 8\,cm`

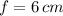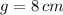
Explanation:

The area of the triangle ADE is:

`A_(ADE) = 60\,cm^(2)-48\,cm^(2)`

`A_(ADE) = 12\,cm^(2)`

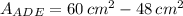
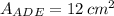
The area of the triangle is defined by the following formula:

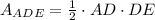`A_(ADE) = (1)/(2)\cdot AD\cdot DE` (1)

If we know that
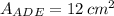`A_(ADE) = 12\,cm^(2)` and
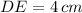`DE = 4\,cm`, then the length of the line segment
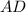`AD` is:

`AD = (2\cdot A_(ADE))/(DE)`

`AD = 6\,cm`

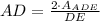
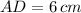
And the area of the rectangle is:

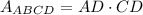`A_(ABCD) = AD\cdot CD` (2)

If we know that
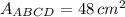`A_(ABCD) = 48\,cm^(2)` and
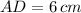`AD = 6\,cm`, then the length of the line segment
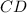`CD` is:

`CD = (A_(ABCD))/(AD)`

`CD = 8\,cm`

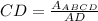
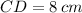
Hence, the values of
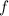`f` and
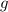`g` are, respectively:

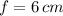`f = 6\,cm`,
`g = 8\,cm`