Question

A company found that monthly reimbursements to their employees could be adequately modeled by a uniform distribution over the interval $10,000 < x < 15,000.

What is the probability of employee reimbursements exceeding $12,000 next month?

Answer 1

0.6 = 60% probability of employee reimbursements exceeding $12,000 next month

Explanation:

A distribution is called uniform if each outcome has the same probability of happening.

The uniform distributon has two bounds, a and b, and the probability of finding a value higher than x is given by:

`P(X > x) = (b - x)/(b - a)`

A company found that monthly reimbursements to their employees could be adequately modeled by a uniform distribution over the interval $10,000 < x < 15,000.

This means that, in thousands of dollars,
`a = 10, b = 15`

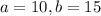
What is the probability of employee reimbursements exceeding $12,000 next month?

`P(X > 12) = (15 - 12)/(15 - 10) = (3)/(5) = 0.6`

0.6 = 60% probability of employee reimbursements exceeding $12,000 next month