Question

Jason inherited a piece of land from his great-uncle. Owners in the area claim that there is a 45% chance that the land has oil. Jason decides to test the land for oil. He buys a kit that claims to have an 80% accuracy rate of indicating oil in the soil. What is the probability that the land has oil and the test predicts it

Answer 1

The probability that the land has oil and the test predicts it is 36%

Explanation:

So option C. 0.36 is correct for plato users

Answer 2

0.36 = 36% probability that the land has oil and the test predicts it

Explanation:

Conditional Probability

We use the conditional probability formula to solve this question. It is

`P(B|A) = (P(A \cap B))/(P(A))`

In which

P(B|A) is the probability of event B happening, given that A happened.

`P(A \cap B)` is the probability of both A and B happening.

P(A) is the probability of A happening.

45% chance that the land has oil.

This means that
`P(A) = 0.45`

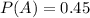
He buys a kit that claims to have an 80% accuracy rate of indicating oil in the soil.

This means that
`P(B|A) = 0.8`

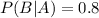
What is the probability that the land has oil and the test predicts it?

This is
`P(A \cap B)`. So

`P(B|A) = (P(A \cap B))/(P(A))`

`P(B \cap A) = P(B|A)*P(A) = 0.8*0.45 = 0.36`

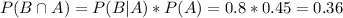
0.36 = 36% probability that the land has oil and the test predicts it