a. There were 5 tourists interviewed.
b. There was 1 tourist who traveled by air only.
Let's denote:
- R as the number of tourists traveling by road,
- A as the number of tourists traveling by air.
According to the information given:
1.
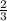 of the tourists traveled by road,
of the tourists traveled by road,
2.
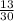 of the tourists traveled by air,
of the tourists traveled by air,
3.
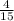 of the tourists traveled by both air and road.
of the tourists traveled by both air and road.
Now, let's calculate the portion of tourists who traveled only by road (\( R \) only):
![\[ \text{Portion traveling only by road} = (2)/(3) - (4)/(15) = (10)/(15) - (4)/(15) = (6)/(15) \]](https://img.qammunity.org/qa-images/2022/formulas/mathematics/high-school/bx0jq8gczdt9sj4069j2ol.png)
Similarly, let's calculate the portion of tourists who traveled only by air (\( A \) only):
![\[ \text{Portion traveling only by air} = (13)/(30) - (4)/(15) = (13)/(30) - (8)/(30) = (5)/(30) \]](https://img.qammunity.org/qa-images/2022/formulas/mathematics/high-school/x47qkgkl1dggd72szh6uup.png)
Now, since 20 tourists did not travel by either air or road, we can set up an equation:
![\[ \text{Portion traveling only by road} + \text{Portion traveling only by air} + \text{Portion traveling by both} + \text{Not traveling at all} = 1 \]](https://img.qammunity.org/qa-images/2022/formulas/mathematics/high-school/ksx0yu1s2egyv3bwabld25.png)
![\[ (6)/(15) + (5)/(30) + (4)/(15) + \text{Not traveling at all} = 1 \]](https://img.qammunity.org/qa-images/2022/formulas/mathematics/high-school/h8tj4iq0uni1e0eealbc2s.png)
Solving for "Not traveling at all":
![\[ \text{Not traveling at all} = 1 - (6)/(15) - (5)/(30) - (4)/(15) \]](https://img.qammunity.org/qa-images/2022/formulas/mathematics/high-school/ldtf08sr9onz7q8co7qpub.png)
![\[ \text{Not traveling at all} = (1)/(5) \]](https://img.qammunity.org/qa-images/2022/formulas/mathematics/high-school/p52l2ltzmqgve8oj3bi6m1.png)
Now, we can find the total number of tourists interviewed (denoted as \( \alpha \)):
![\[ \alpha = \frac{1}{\text{Not traveling at all}} = (1)/((1)/(5)) = 5 \]](https://img.qammunity.org/qa-images/2022/formulas/mathematics/high-school/6l3uowl4ch15odl9vtew9j.png)
So, there were 5 tourists interviewed.
Now, to find the number of tourists who traveled by air only (denoted as \( \beta \)):
![\[ \beta = \text{Portion traveling only by air} * \alpha = (5)/(30) * 5 = 1 \]](https://img.qammunity.org/qa-images/2022/formulas/mathematics/high-school/e5d2mckzr3xhxt7lntct71.png)
So, there was 1 tourist who traveled by air only.
The following question may be like this:
A number of tourists were interviewed on their choice of means of travel. Two-thirds said that they travelled by road, 13/30 by air and 4/15 by both air and road. If 20 tourists did not travelled by either air or road. i. how many tourists α) were interviewed β) travelled by air only?