Answer:
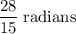 , which is approximately
, which is approximately
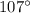 .
.
Explanation:
In a given circle, the angle of a sector is proportional to the length of the corresponding arc:
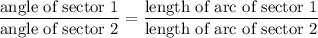 .
.
For the circle in this question,
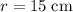 , and the circumference would be:
, and the circumference would be:
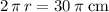 .
.
The full circle itself is like a sector with an angle of
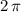 , with the arc length equal to the circumference of the circle.
, with the arc length equal to the circumference of the circle.
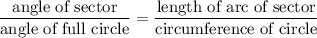 .
.
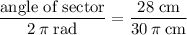 .
.
Rearrange the equation to find the angle of the sector:
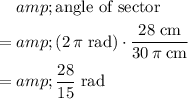 .
.
In other words, the angle of this sector would be
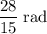 . Multiply that measure in radians by
. Multiply that measure in radians by
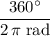 to find the value of the angle measured in degrees:
to find the value of the angle measured in degrees:
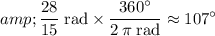 .
.