Question

An arc 28 cm is cut from a circle of radius 15 cm. Find the angle of the sector formed by this arc.

Answer 1

`\displaystyle (28)/(15)\; \text{radians}`, which is approximately
`107^(\circ)`.

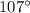Explanation:

In a given circle, the angle of a sector is proportional to the length of the corresponding arc:

`\displaystyle \frac{\text{angle of sector $1$}}{\text{angle of sector $2$}} = \frac{\text{length of arc of sector $1$}}{\text{length of arc of sector $2$}}`.

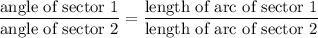For the circle in this question,
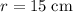`r = 15\; \rm cm`, and the circumference would be:

`2\, \pi \, r = 30\, \pi\; \rm cm`.

The full circle itself is like a sector with an angle of
`2\, \pi`, with the arc length equal to the circumference of the circle.

`\displaystyle \frac{\text{angle of sector}}{\text{angle of full circle}} = \frac{\text{length of arc of sector}}{\text{circumference of circle}}`.

`\displaystyle \frac{\text{angle of sector}}{2\,\pi\; \rm rad} = (28\; \rm cm)/(30\, \pi\; \rm cm)`.

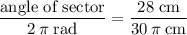Rearrange the equation to find the angle of the sector:

`\begin{aligned} & \text{angle of sector} \\ =\; & (2\,\pi\; \rm rad) \cdot (28\; \rm cm)/(30\, \pi\; \rm cm) \\ =\; & (28)/(15)\; \rm rad\end{aligned}`.

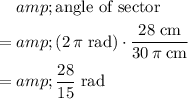In other words, the angle of this sector would be
`\displaystyle (28)/(15)\; \rm rad`. Multiply that measure in radians by
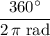`\displaystyle (360^(\circ))/(2\,\pi\; \rm rad)` to find the value of the angle measured in degrees:

`\begin{aligned} & (28)/(15)\; \rm rad * (360^(\circ))/(2\,\pi\; \rm rad) \approx 107^(\circ)\end{aligned}`.