Question

How many moles are in 58.6 L of N2gas at STP?

Answer 1

n equals 2.62 hope this helps

Answer 2

`\boxed {\boxed {\sf 2.62 \ mol \ N_2}}`

Step-by-step explanation:

The relationship between moles and gases is unique. Regardless of the type of gas, there will always be 22.4 liters of gas in 1 mole, as long as it's at STP (standard temperature and pressure).

We can make a ratio using this information.

`\frac {22.4 \ L \ N_2}{ 1 \ mol \ N_2}`

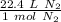
Multiply by the given number of moles.

`58.6 \ L \ N_2 *\frac {22.4 \ L \ N_2}{ 1 \ mol \ N_2}`

Flip the fraction so the liters of nitrogen cancel.

`58.6 \ L \ N_2 *\frac {1 \ mol \ N_2}{ 22.4 \ L \ N_2}`

`58.6 *\frac {1 \ mol \ N_2}{ 22.4 }`

`\frac {58.6 \ mol \ N_2}{ 22.4 }= 2.61607143 \ mol \ N_2`

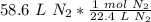
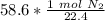
The original measurement of liters has 3 significant figures, so our answer must have the same.

For the number of moles calculated, 3 sig figs is the hundredth place. The 6 in the thousandth place tells us to round the 1 to a 2.

`2.62 \ mol \ N_2`

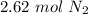
58.6 liters of N₂ gas at STP is equal to about 2.62 moles.