Question

Find the coefficient of a^5b^4 in (3a-b/3)^9

(question 2 a. ii on the picture)
need it asap!

Answer 1

378

Explanation:

ii. We use the binomial theorem which states that,

`(a + b) {}^(n) = \binom{n}{0} a {}^(n) b {}^(0) + \binom{n}{1} a {}^(n - 1) b {}^(1) + \binom{n}{2} a {}^(n - 2) b {}^(2) + \binom{n}{3} a {}^(n - 3) b {}^(3) + ...... \binom{n}{n - 2} a {}^(2) b {}^(n - 2) + \binom{n}{n - 1} {a}^(1) b {}^(n - 1) + \binom{n}{n} a {}^(0) {b}^(n)`

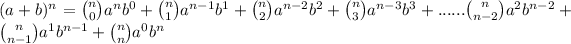
I'll explain in depth if you want me to.

We have

`(3a - (b)/(3) ) {}^(9)`

We must find the coeffeicent that include term.

`{a}^(5) b {}^(4)`

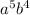
The first term of the binomial expansion is a which has a degree 9 and b has a degree of 0. and since the term, a has a^5 and b^4. here this must that 9 must choose 4.

So let do the combinations formula,

`\binom{9}{4} = (9 * 8 * 7 * 6 * 5 * 4 * 3 * 2 * 1)/((4 * 3 * 2 * 1)(5 * 4 * 3 * 2 * 1))`

`\binom{9}{4} = (9 * 8 * 7 * 6)/(4 * 3 * 2 * 1)`

`\binom{9}{4} = 126`

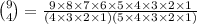
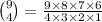
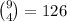
So during that point our expansion will include.

`126(3a) {}^(5) ( - (b)/(3) ) {}^(4)`

`126(243 {a}^{ {5} } * \frac{b {}^(4) }{81} ) = 126(3a {}^(5) b {}^(4) )`

`378 {a}^(5) {b}^(4)`

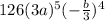
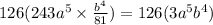
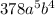
So the coeffeicent is 378