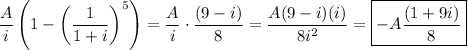Question

Please help me! How this formula transform in this formula plssss. Show me the solving steps plss ​

Answer 1

9514 1404 393

Answer:

• (-A/8)(1+9i)
• (-A/8)(1+9i)

Explanation:

Let's start with the expression 1/(1+i). It is simplified by multiplying numerator and denominator by its conjugate.

`(1)/(1+i)=(1-i)/((1+i)(1-i))=(1-i)/(2)`

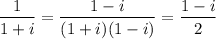
Subtracting this from 1, as in the denominator inside parentheses, gives its conjugate.

`1-(1-i)/(2)=(1+i)/(2)`

__

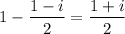
The 5th power can be found a couple of ways. One is to use the binomial expansion. Another is to use Euler's formula. The latter can be somewhat easier.

`(1-i)/(2)=(1)/(√(2))\angle-\!45^(\circ)\\\\\left((1-i)/(2)\right)^5=(1)/(√(2^5))\angle(5(-45^(\circ)))=(1)/(4√(2))(\cos(135^(\circ))+i\sin(135^(\circ)))\\\\=(1)/(8)(-1+i)`

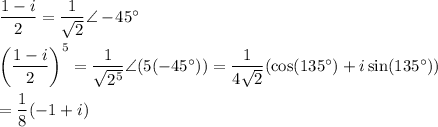
With these parts, we can now write the first expression as ...

`\displaystyle(A)/(i+i)\left((1-((1)/(1+i))^5)/(1-((1)/(1+i)))\right)=A\left((1-i)/(2)\right)\left((1-(-1+i)/(8))/((1+i)/(2))\right)=(A)/(8)\cdot(1-i)/(1+i)\cdot(9-i)\\\\=(A)/(8)\cdot((1-i)^2(9-i))/(1^2-i^2)=(A(-2i)(9-i))/(8\cdot2)=\boxed{-A((1+9i))/(8)}`

__

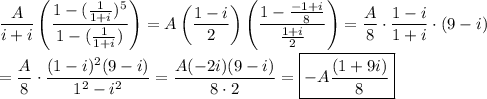
Using the same parts, we can simplify the second expression.

`\displaystyle(A)/(i)\left(1-\left((1)/(1+i)\right)^5\right)=(A)/(i)\cdot((9-i))/(8)=(A(9-i)(i))/(8i^2)=\boxed{-A((1+9i))/(8)}`