Question

What if this function simplified?

Answer 1

Hi!

Let's first expand the cotangent of theta.

You'll probably know that tangent will be "y/x", or
`(sin(x))/(cos(x))`, and cotangent is the reciprocal of this, meaning that it is "x/y" or
`(cos(x))/(sin(x))`.

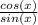That means that we are now given this equation.

`cos(x)(cos(x))/(sin(x))+sin(x)`

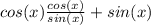
That'll multiply to:

`(cos^2(x))/(sin(x))+sin(x)`

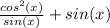
We'll want a common denominator to add by multiplying
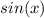`sin(x)` to both top and bottom of the second term:

`(cos^2(x))/(sin(x))+(sin^2(x))/(sin(x))`

`(cos^2(x)+sin^2(x))/(sin(x))`

Pythagorean Identity states that
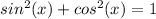`sin^2(x)+cos^2(x)=1`, so substitute that in:

`(1)/(sin(x))`

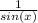
Which simplifies to:

`csc(x)`

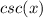
Hope this helps!