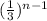Answer:
see explanation
Explanation:
(a)
Using the recursive rule and a₁ = 15 , then
a₂ = a₁ - 3 = 15 - 3 = 12
a₃ = a₂ - 3 = 12 - 3 = 9
a₄ = a₃ - 3 = 9 - 3 = 6
The sequence is 15, 12, 9, 6, ....
This is an arithmetic sequence with n th term ( explicit rule )
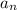 = a₁ + (n - 1)d
= a₁ + (n - 1)d
where a₁ is the first term and d the common difference
Here a₁ = 15 and d = - 3 , then
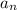 = 15 - 3(n - 1) = 15 - 3n + 3 = 18 - 3n
= 15 - 3(n - 1) = 15 - 3n + 3 = 18 - 3n
----------------------------------------------------------------------
(b)
Using the recursive rule and t₁ = 108 , then
t₂ =
 t₁ =
t₁ =
 × 108 = 36
× 108 = 36
t₃ =
 t₂ =
t₂ =
 × 36 = 12
× 36 = 12
t₄ =
 t₃ =
t₃ =
 × 12 = 4
× 12 = 4
The sequence is 108, 36, 12, 4, ......
This is a geometric sequence with n th term
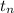 = t₁
= t₁
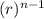
where t₁ is the first term and r the common ratio
Here t₁ = 108 and r =
 , then
, then
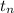 = 108
= 108