Question

How do you write the equation of a line (in slope intercept form) with three given points?​

Answer 1

You only need two points to write the equation of a line.

Slope intercept form of a line is y=mx+b, where m is the slope and b is the y intercept.

I’m going to use the points (5,3) and (8,5) to show how to write the equation.

First, find the slope. The formula to find the slope is y2-y1/x2-x1. With my points, the slope equation would look like this:
m=(5-3)/(8-5)
m=2/3

I put this into my point slope formula
y=2/3x+b

To find out the b (y-intercept), I plug in one pair of points, then solve for b. I will use (5,3)

3=2/3(5)+b
3=10/3+b
-1/3=b

I can now add b to my equation, and get y=2/3x-1/3

To double check this, I could graph this line and make sure that it crosses my selected points. Hope this helps!

Answer 2

With even just two points, you can find the equation of a line in slope-intercept form.

Slope-intercept form:
`y=mx+b` where
`m` is the slope and
`b` is the y-intercept

1) Solve for the slope (
`m`)

The equation to solve for the slope is
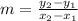`m=(y_2-y_1)/(x_2-x_1)` when the two points are
`(x_1,y_1)` and
`(x_2,y_2)`. Plug the coordinates of these points into the equation and solve for
`m`.

Then, plug
`m` into
`y=mx+b`.

1) Solve for the y-intercept (
`b`)

Then, take any of the given points and plug it into
`y=mx+b` along with the slope. Isolate
`b` to get the y-intercept. Then, plug both m and b back into
`y=mx+b` to get your final equation.

I hope this helps!