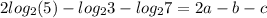Question

If log2 5 = a, log2 3 = b and log2 7 = c, determine an expression for log2 (25/21) in terms of a, b, and c

Answer 1

`2a - b -c`

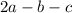
Step-by-step explanation: We know that:

`log_(2) 5 = a\\log_(2) 3 = b\\log_2 7 = c\\`

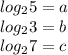
and we want:

`log_2 (25)/(21)`.

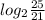We can form the numerator using just the first fact (since 5^2 is 25) and the denominator using the latter two (since 3*7 = 21).

`log_2 (25)/(21) = log_2 (5^2)/(3*7).`

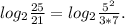
The logarithm of a division can be expanded by subtracting the numerator and denominator (while still keeping the log). The logarithm of a product can be expanded by adding the terms while keeping the log. If the logarithm is raised to a power, we can bring it down as a factor:

`log_2 (5^2)/(3*7) = log_2(5)^2 - log_2 (3*7) = 2 log_2(5) - (log_2 3 + log_2 7)`

`= 2 log_2(5) - log_2 3 - log_2 7` .

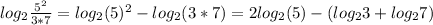
Substituting the variables:

`2 log_2(5) - log_2 3 - log_2 7 = 2a - b - c`