Answer:
- Q1. 37.3 cm
- Q2. (a) 8.66 cm (b) 17.3 cm
Explanation:
Question 1
Given
- Chord 1 c1 = 36 cm
- Chord 2 c2 = 30 cm
- Radius r = d/2 = 50/2 = 25 cm
- Chords are parallel
To find
- The distance between the chords
Solution
The distance between the chords is sum of the distances between the center and the midpoint of the chords
The segments between the center to the midpoints of the chords for right triangles with one side being the radius.
The distance is:
- h = h1 + h2
- h1 =
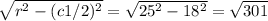 ≈ 17.3 cm (rounded)
≈ 17.3 cm (rounded) - h2 =
 = 20 cm
= 20 cm - h = 17.3 + 20 = 37.3 cm
------------------------------------------
Question 2
Given
- Equilateral triangle inscribed into circle
- Side of the triangle is 30 cm
To find
- Distance between the center and the side
- Radius
Solution
Midpoint of the side, the center and the vertex form a right triangle with 30° angle at the vertex.
Let the radius be r, the distance from the center to the side be h
Then we have:
As per property of 30°-60°=90° triangle, the side opposite to 30° is half of the hypotenuse. In this case, h = r/2 or r = 2h
Substitute r into equation above and solve for h:
- (2h)² = h² + 225
- 3h² = 225
- h² = 75
- h = √75 = 8.66 cm (rounded)
Find the value of r:
- r = 2*8.66 = 17.3 cm (rounded)