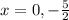Question

How do I solve equations with a variable to the power of something (give steps please)

Like these.

`2x^2+5x=0`

Answer 1

`x = 0, -(5)/(2)`

Explanation:

First move all terms to one side of the equation to set them equal to 0

That is already done in your problem

The try to factor, if possible. In your case, factor out x

x(2x + 5) = 0 Now, use the property that says if AB = 0, then A = 0 or B = 0 or both A and B equal 0

So, x = 0 or 2x + 5 = 0

2x = -5

x =
`-(5)/(2)`

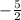
Always check your results in the original equation to see if they work

`2(0^(2) + 5(0) = 0 + 0 = 0\\`

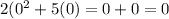
and
`2(-(5)/(2) )^(2) + 5(-(5)/(2) )\\ = 2((25)/(4) ) - (25)/(2) \\ = (25)/(2) - (25)/(2) = 0`

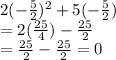
Both results make the equation true, so
`x = 0, -(5)/(2)`

Answer 2

Explanation:

Factoring will reveal the solution. So we divide the equation by the greatest common factor of the terms and use that factor as the coefficient. In this case the greatest common factor is just x.

2x^2+5x

x(2x+5) so the equation will equal zero when either of those expressions is zero because zero times anything is zero. x=0 and x=-5/2