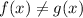Answer: d) -3
==========================================================
Step-by-step explanation:
When f(x) = g(x) is true, this is where the two graphs intersect. So we have three solutions here because we have three different intersection points.
The x coordinates of those intersection points, from left to right, are: -3/2, 0, 3.
Note: -3/2 = -1.5 is exactly at the midpoint of -2 and -1.
In other words, if we plugged in x = 0 into both f(x) and g(x), then we'll get the same output value and hence f(x) = g(x) will be true. The same applies to -3/2 and 3 as well.
Recall that y = f(x) and y = g(x), so saying f(x) = g(x) really means they both have the same y outputs for that specific input x value. This explains why intersection points correspond to solutions.
------------
Since x = -3 is not on the list of solutions, this means this x value will make f(x) and g(x) be different outputs. The graph shows the curves do not intersect with each other when x = -3. Instead, g(x) is above f(x) at this location. So we can say g(x) > f(x) when x = -3.
In short, when x = -3, we have