Question

13. Write

y = 2x^2 -12x+16 in vertex form.

Please show work if possible so I know how to do it

Answer 1

First off, we factor out the expression:

`\displaystyle \large{y = 2 {x}^(2) - 12x + 16} \\ \displaystyle \large{y = 2 ( {x}^(2) - 6x + 8) }`

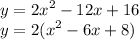
In the bracket, separate 8 out of the expression.

`\displaystyle \large{y = 2[ ( {x}^(2) - 6x + 8)] }\\ \displaystyle \large{y = 2[ ( {x}^(2) - 6x) + 8]}`

In x^2-6x, find the third term that can make up or convert it to a perfect square form. The third term is 9 because:

`\displaystyle \large{ {(x - 3)}^(2) = {x}^(2) - 6x + 9}`

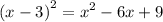
So we add +9 in x^2-6x.

`\displaystyle \large{y = 2[ ( {x}^(2) - 6x + 9) + 8]}`

Convert the expression in the small bracket to perfect square.

`\displaystyle \large{y = 2[ {(x - 3)}^(2) + 8]}`

Since we add +9 in the small bracket, we have to subtract 8 with 9 as well.

`\displaystyle \large{y = 2[ {(x - 3)}^(2) + 8 - 9]} \\ \displaystyle \large{y = 2[ {(x - 3)}^(2) - 1]}`

Then we distribute 2 in.

`\displaystyle \large{y = 2[ {(x - 3)}^(2) - 1]} \\`

`\displaystyle \large{y = 2[ {(x - 3)}^(2) - 1]} \\ \displaystyle \large{y = [2 * {(x - 3)}^(2) ]+[ 2 * ( - 1)] } \\ \displaystyle \large{y = 2 {(x - 3)}^(2) - 2 }`

Remember that negative multiply positive = negative.

Hence the vertex form is y = 2(x-3)^2-2 or first choice.