There are some symbols missing in your integral. I suspect you meant something along the lines of
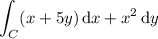
but we can consider a more general integral,
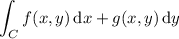
One way to compute the integral is to split up C into two component paths C₁ and C₂, parameterize both, directly compute the integral over each path, then sum the results.
Parameterize C₁ and C₂ respectively by
〈x₁(t), y₁(t)⟩ = (1 - t ) 〈0, 0⟩ + t 〈5, 1⟩ = 〈5t, t⟩
〈x₂(t), y₂(t)⟩ = (1 - t ) 〈5, 1⟩ + t 〈5, 0⟩ = 〈5, 1 - t⟩
where 0 ≤ t ≤ 1. Then
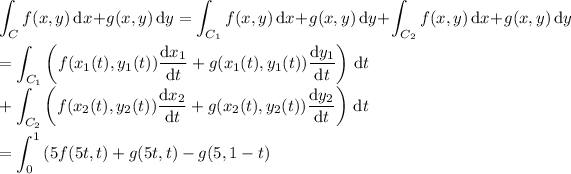
If f and g agree with what I suggested earlier, the integral reduces to
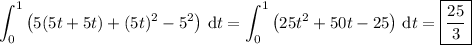
Another way would be to close the path with a line segment from (5, 0) to (0, 0) and apply Green's theorem. Compute the resulting double integral, then subtract the contribution of the line integral over this third line segment. Provided that f(x,y) and g(x,y) don't have any singularities along this closed path C* or inside the triangle (call it T ) that it surrounds, we have
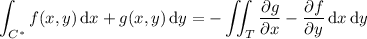
where T is the region,
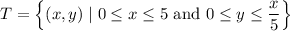
The double integral has a negative sign because C* has a negative, clockwise orientation.
Then
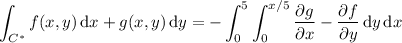
If f and g are as I suggested, then
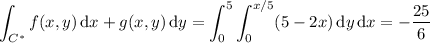
From this, we subtract the integral along the line segment C₃ from (5, 0) to (0, 0), parameterized by
〈x₃(t), y₃(t)⟩ = (1 - t ) 〈5, 0⟩ + t 〈0, 0⟩ = 〈5 - 5t, 0⟩
again with 0 ≤ t ≤ 1.
Then the remaining line integral is
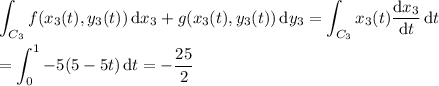
and so the original line integral is again -25/6 - (-25/2) = 25/3.