Question

Question 1. (20 points) Evaluate the line integral Z C (x 5y) dx x 2 dy where C consists of the two line segments from (0, 0) to (5, 1) and from (5, 1) to (5, 0).

Answer 1

There are some symbols missing in your integral. I suspect you meant something along the lines of

`\displaystyle \int_C (x+5y)\,\mathrm dx + x^2\,\mathrm dy`

but we can consider a more general integral,

`\displaystyle \int_C f(x,y)\,\mathrm dx + g(x,y)\,\mathrm dy`

One way to compute the integral is to split up C into two component paths C₁ and C₂, parameterize both, directly compute the integral over each path, then sum the results.

Parameterize C₁ and C₂ respectively by

〈x₁(t), y₁(t)⟩ = (1 - t ) 〈0, 0⟩ + t 〈5, 1⟩ = 〈5t, t⟩

〈x₂(t), y₂(t)⟩ = (1 - t ) 〈5, 1⟩ + t 〈5, 0⟩ = 〈5, 1 - t⟩

where 0 ≤ t ≤ 1. Then

`\displaystyle \int_C f(x,y)\,\mathrm dx + g(x,y)\,\mathrm dy = \int_(C_1) f(x,y)\,\mathrm dx + g(x,y)\,\mathrm dy + \int_(C_2) f(x,y)\,\mathrm dx + g(x,y)\,\mathrm dy \\\\ = \int_(C_1) \left(f(x_1(t),y_1(t))(\mathrm dx_1)/(\mathrm dt) + g(x_1(t),y_1(t))(\mathrm dy_1)/(\mathrm dt)\right)\,\mathrm dt \\ + \int_(C_2) \left(f(x_2(t),y_2(t))(\mathrm dx_2)/(\mathrm dt) + g(x_2(t),y_2(t))(\mathrm dy_2)/(\mathrm dt)\right)\,\mathrm dt \\\\ = \int_0^1 \left(5f(5t,t) + g(5t,t) - g(5,1-t)`

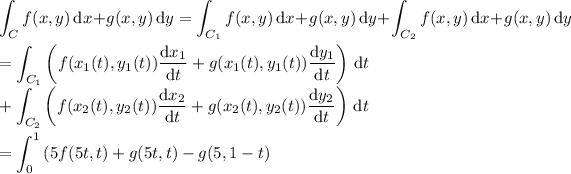
If f and g agree with what I suggested earlier, the integral reduces to

`\displaystyle \int_0^1 \left(5(5t+5t) + (5t)^2 - 5^2\right)\,\mathrm dt = \int_0^1 \left(25t^2 + 50t - 25\right)\,\mathrm dt = \boxed{\frac{25}3}`

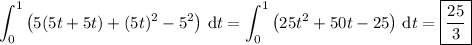
Another way would be to close the path with a line segment from (5, 0) to (0, 0) and apply Green's theorem. Compute the resulting double integral, then subtract the contribution of the line integral over this third line segment. Provided that f(x,y) and g(x,y) don't have any singularities along this closed path C* or inside the triangle (call it T ) that it surrounds, we have

`\displaystyle \int_(C^*) f(x,y)\,\mathrm dx + g(x,y)\,\mathrm dy = -\iint_T (\partial g)/(\partial x)-(\partial f)/(\partial y) \,\mathrm dx\,\mathrm dy`

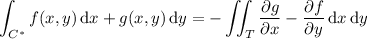
where T is the region,

`T = \left\{(x,y) \mid 0\le x\le 5 \text{ and } 0\le y\le \frac x5\right\}`

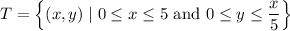
The double integral has a negative sign because C* has a negative, clockwise orientation.

Then

`\displaystyle \int_(C^*) f(x,y)\,\mathrm dx + g(x,y)\,\mathrm dy = -\int_0^5\int_0^(x/5) (\partial g)/(\partial x)-(\partial f)/(\partial y) \,\mathrm dy\,\mathrm dx`

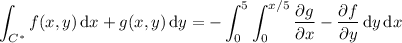
If f and g are as I suggested, then

`\displaystyle \int_(C^*) f(x,y)\,\mathrm dx + g(x,y)\,\mathrm dy = \int_0^5\int_0^(x/5) (5-2x) \,\mathrm dy\,\mathrm dx = -\frac{25}6`

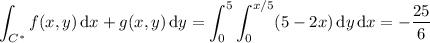
From this, we subtract the integral along the line segment C₃ from (5, 0) to (0, 0), parameterized by

〈x₃(t), y₃(t)⟩ = (1 - t ) 〈5, 0⟩ + t 〈0, 0⟩ = 〈5 - 5t, 0⟩

again with 0 ≤ t ≤ 1.

Then the remaining line integral is

`\displaystyle \int_(C_3) f(x_3(t),y_3(t))\,\mathrm dx_3 + g(x_3(t),y_3(t))\,\mathrm dy_3 = \int_(C_3) x_3(t)(\mathrm dx_3)/(\mathrm dt)\,\mathrm dt \\\\ = \int_0^1 -5(5-5t)\,\mathrm dt = -\frac{25}2`

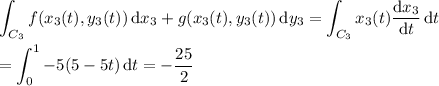
and so the original line integral is again -25/6 - (-25/2) = 25/3.