Question

`\sqrt[4]{5x/8y}`i asked my teacher and she said this "Hi there. separate the radicals - numerator and denominator first. Then, you'll need to make "8" into 2^3. You'll want to create a group of 4 for both the 2 and the y in the denominator, because your index is "4". So, you'll need one more "2" and "y^3". Then you multiply top and bottom by the 4th root of 2y^3 and simplify from there." can you show me what to do

Answer 1

Answer:
`\frac{\sqrt[4]{10xy^3}}{2y}`

where y is positive.

The 2y in the denominator is not inside the fourth root

==================================================

Work Shown:

`\sqrt[4]{(5x)/(8y)}\\\\\\\sqrt[4]{(5x*2y^3)/(8y*2y^3)}\ \ \text{.... multiply top and bottom by } 2y^3\\\\\\\sqrt[4]{(10xy^3)/(16y^4)}\\\\\\\frac{\sqrt[4]{10xy^3}}{\sqrt[4]{16y^4}} \ \ \text{ ... break up the fourth root}\\\\\\\frac{\sqrt[4]{10xy^3}}{\sqrt[4]{(2y)^4}} \ \ \text{ ... rewrite } 16y^4 \text{ as } (2y)^4\\\\\\\frac{\sqrt[4]{10xy^3}}{2y} \ \ \text{... where y is positive}\\\\\\`

The idea is to get something of the form
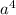`a^4` in the denominator. In this case,
`a = 2y`

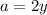
To be able to reach the
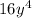`16y^4`, your teacher gave the hint to multiply top and bottom by
`2y^3`

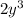
For more examples, search out "rationalizing the denominator".

Keep in mind that
`\sqrt[4]{(2y)^4} = 2y` only works if y isn't negative.

If y could be negative, then we'd have to say
`\sqrt[4]{(2y)^4} = |2y|`. The absolute value bars ensure the result is never negative.

Furthermore, to avoid dividing by zero, we can't have y = 0. So all of this works as long as y > 0.