Question

Prove that the square of an odd number is always 1 more than a multiple of 4.

Input note: use 2n +1 as your odd number, and leave your answer in the form
4(...) +1
(4 marks)

Answer 1

See explanation.

Explanation:

If the odd number is 2n+1 note that n can be any number because any even number plus one will be odd. Let's start by squaring 2n+1 to get:

`4n^2+4n+1`

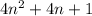
Consider xy (x times y). xy is a multiple of both x and y because xy/x = y and xy/y = x. So it doesn't matter what n is it will be a multiple of 4. So now we know that 4n^2 and 4n are both multiples of 4. If we add them together, it will still be a multiple of 4. 2x + 4x = 6x and 6x is still divisible by x.

Now the plus 1 will always make it so it will be one more than a multiple of 4.