Question

The perimeter of a triangle is 300 m . If its sides are in the ratio 3:5:7. Find the area of the triangle.

Plzz answer fast.
​

Answer 1

If the perimeter = 300m

let the ratio be in x

a/q.

3x + 5x + 7x. = 300m

15x = 300

x = 300/15

x = 20

hence angles are

60 , 100 and 140

hope it helps

Answer 2

A ≈ 1500
`√(3)` m²

Explanation:

sum the parts of the ratio, 3 + 5 + 7 = 15 parts

Divide perimeter by 15 to find the value of one part of the ratio.

300 ÷ 15 = 20 m ← value of 1 part of the ratio , then

3 parts = 3 × 20 = 60 m

5 parts = 5 × 20 = 100 m

7 parts = 7 × 20 = 140 m

The 3 sides of the triangle are 60 m, 100 m , 140 m

To calculate the area (A) having all 3 sides use Hero's formula

A =
`√(s(s-a)(s-b)(s-c))`

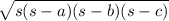
where s is the semiperimeter and a, b , c the sides of the triangle

s = 300 m ÷ 2 = 150 m

let a = 60, b = 100 and c = 140 , then

A =
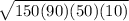
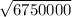
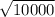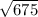
`√(150(150-60)(150-100)(150-140))`

=
`√(150(90)(50)(10))`

=
`√(6750000)`

=
`√(10000)` ×
`√(675)`

= 100 ×
`√(25(27))`

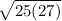
= 100 × 5
`√(27)`

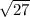
= 500 ×
`√(9(3))`

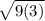
= 500 × 3
`√(3)`

= 1500
`√(3)` m²