Question

if a person can jump maximum along distance of 3m ,on the earth how far could be jump on the moon where acceleration due to gravity is 1÷16 of that on the earth​

Answer 1

The person can jump 48 m on the Moon

Step-by-step explanation:

The question parameters are;

The maximum long jump distance of a person on Earth,
`R_(max)` = 3 m

The acceleration due to gravity on the Moon = 1 ÷ 16 of that on Earth

The distance the person can jump on the Moon is given as follows;

A person performing a jump across an horizontal distance on Earth (under gravitational force) follows the path of the motion of a projectile

The horizontal range,
`R_(max)`, of a projectile motion is found by using the following formula

`R_(max) = (u^2)/(g)`

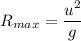
Where;

g = The acceleration due to gravity = 9.8 m/s²

Therefore, we have;

`R_(max) = 3 \, m = (u^2)/(9.8 \, m/s^2 )`

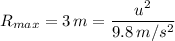
u² = 3 m × 9.8 m/s² = 29.4 m²/s²

Therefore, on the Moon, we have;

The acceleration due to gravity on the Moon,
`g_(Moon)` = 1/16 × g

∴
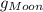`g_(Moon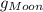)` = 1/16 × g = 1/16 × 9.8 m/s² ≈ 0.6125 m/s²

`R_(max \ Moon) = (u^2)/(g_(Moon)) = (29.4 \ m^2/s^2)/(0.6125 \, m/s^2 ) \approx 48 \, m`

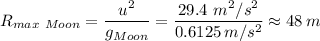
The maximum distance the person can jump on the Moon with the same velocity which was used on Earth is
`R_(max \ Moon)` ≈ 48 m