Answer:
The system of equations has no solution.
Explanation:
Let the following system of linear equations:
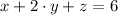 (1)
(1)
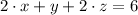 (2)
(2)
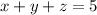 (3)
(3)
Since the quantity of equations and variables are the same, there is only one solution to this system. First, we clear
 in (3):
in (3):
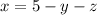
And make substitution both in (1) and (2):
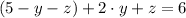
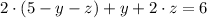
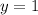 (4)
(4)
 (5)
(5)
Which lead to a contradiction, since
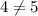 . Therefore, the system of linear equations has no solution.
. Therefore, the system of linear equations has no solution.