Given:
The point (7, 4) lies on a circle centered at the origin.
To find:
The equation of the circle and the radius of the circle.
Solution:
Distance formula:
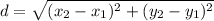
The point (7, 4) lies on a circle centered at the origin. So, the distance between the points (7,4) and (0,0) is equal to the radius of the circle.
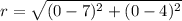
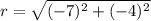
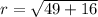
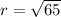
The standard form of the circle is
 ...(i)
...(i)
Where, (h,k) is the center of the circle and r is the radius of the circle.
Putting h=0, k=0 and
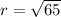 in (ii), we get
in (ii), we get


Therefore, the equation of the circle is
 and its radius is
and its radius is
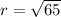 .
.