Question

Someone help please

Answer 1

Answer: Choice A

`\tan(\alpha)*\cot^2(\alpha)\\\\`

============================================================

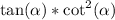
Step-by-step explanation:

Recall that
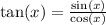`\tan(x) = (\sin(x))/(\cos(x))` and
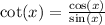`\cot(x) = (\cos(x))/(\sin(x))`. The connection between tangent and cotangent is simply involving the reciprocal

From this, we can say,

`\tan(\alpha)*\cot^2(\alpha)\\\\\\(\sin(\alpha))/(\cos(\alpha))*\left((\cos(\alpha))/(\sin(\alpha))\right)^2\\\\\\(\sin(\alpha))/(\cos(\alpha))*(\cos^2(\alpha))/(\sin^2(\alpha))\\\\\\(\sin(\alpha)*\cos^2(\alpha))/(\cos(\alpha)*\sin^2(\alpha))\\\\\\(\cos^2(\alpha))/(\cos(\alpha)*\sin(\alpha))\\\\\\(\cos(\alpha))/(\sin(\alpha))\\\\`

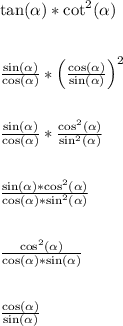
In the second to last step, a pair of sine terms cancel. In the last step, a pair of cosine terms cancel.

All of this shows why
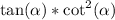`\tan(\alpha)*\cot^2(\alpha)\\\\` is identical to
`(\cos(\alpha))/(\sin(\alpha))\\\\`

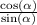
Therefore,
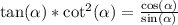`\tan(\alpha)*\cot^2(\alpha)=(\cos(\alpha))/(\sin(\alpha))\\\\` is an identity. In mathematics, an identity is when both sides are the same thing for any allowed input in the domain.

You can visually confirm that
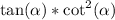`\tan(\alpha)*\cot^2(\alpha)\\\\` is the same as
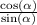`(\cos(\alpha))/(\sin(\alpha))\\\\` by graphing each function (use x instead of alpha). You should note that both curves use the exact same set of points to form them. In other words, one curve is perfectly on top of the other. I recommend making the curves different colors so you can distinguish them a bit better.