Answer:
D. 10^10
Explanation:
Multiplying numbers with exponents rule :
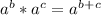
explanation of rule : we simply keep the bases the same and add the exponents.
10^3 • 10^7
keep the base as 10 and add the exponents
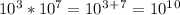
Keep in mind that this only works when the bases are the same.