Question

Pls helpp!!

the angles of a quadrilateral are x°, (x+5)°, (2x-25)° and (x+10)°
find the value of x​

Answer 1

Given:

The angles of a quadrilateral are x°, (x+5)°, (2x-25)° and (x+10)°.

To find:

The value of x.

Solution:

We know that the sum of all interior angles of a quadrilateral is 360°. So,

`x^\circ+(x+5)^\circ+(2x-25)^\circ+(x+10)^\circ=180^\circ`

`(5x-10)^\circ=180^\circ`

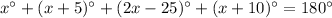
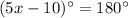
It can be written as

`(5x-10)=180`

`5x=180+10`

`5x=190`

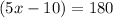
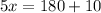
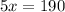
Divide both sides by 5.

`x=(190)/(5)`

`x=38`

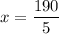
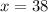
Therefore, the value of x is 38.