Answer:
846.06 units
Explanation:
The amount of profit, y, made by the company, is related to the selling price of each widget, x, by the given equation as follows :
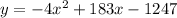 ...(1)
...(1)
We need to find out the maximum amount of profit the company can make.
For maximum profit put dy/dx = 0
So,
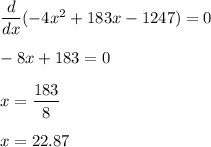
Put x = 22.87 in equation (1). So,
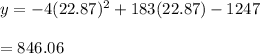
So, the maximum profit is 846.06 units.