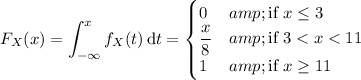Question

A continuous random variable is uniformly distributed in the interval a<X<b the Lower quartile is 5 and upper quartile is 9 find

a. the values of a and b
b. p(6<X<7)
c. the cumulative distributive function

راز​

Answer 1

(a) X has a probabiliity density of

`f_X(x) = \begin{cases}\frac1{b-a}&\text{if }a<x<b\\0&\text{otherwise}\end{cases}`

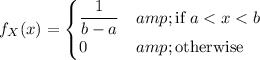
If the lower quartile is 5 and the upper quartile is 9, then

`\displaystyle \int_a^5 f_X(x)\,\mathrm dx = 0.25 \text{ and } \int_9^b f_X(x)\,\mathrm dx = 0.25`

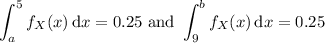
Computing the integrals gives the following system of equations:

`\displaystyle \int_a^5(\mathrm dx)/(b-a) = (5-a)/(b-a) = 0.25 \\\\ \int_9^b (\mathrm dx)/(b-a) = (b-9)/(b-a) = 0.25`

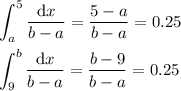
5 - a = 0.25 (b - a) ==> 0.75a + 0.25b = 5 ==> 3a + b = 20

b - 9 = 0.25 (b - a) ==> 0.25a + 0.75b = 9 ==> a + 3b = 36

Eliminate a :

(3a + b) - 3 (a + 3b) = 20 - 3×36

-8b = -88

==> b = 11 ==> a = 3

and so P(X = x) = 1/(11 - 3) = 1/8 for all 3 < x < 11.

(b)

`\displaystyle P(6<X<7) = \int_6^7f_X(x)\,\mathrm dx = \int_6^7\frac{\mathrm dx}8 = \boxed{\frac18}`

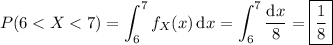
(c) The distribution function is then

`\displaystyle F_X(x) = \int_(-\infty)^x f_X(t)\,\mathrm dt = \begin{cases}0&\text{if }x\le3 \\ \frac x8 &\text{if }3<x<11 \\ 1&\text{if }x\ge11\end{cases}`