Question

I need help!! ASAP!!

Simplify the complex fraction. State the conditions under which the expression is undefined.

Answer 1

9514 1404 393

Answer:

(2x +1)/(4x^2) . . . . except x=0, -1

Explanation:

Addition of fractions works in the usual way:

a/b +c/d = (ad +bc)/(bd)

Division of fractions works in the usual way:

(a/b)/(c/d) = (ad)/(bc)

__

`(\left((1)/(2x)+(1)/(2x+2)\right))/(\left((2x)/(x+1)\right))=(1)/(2)\cdot(\left((1)/(x)+(1)/(x+1)\right))/(\left((2x)/(x+1)\right))=(1)/(2)\cdot(\left((2x+1)/(x(x+1))\right))/(\left((2x^2)/(x(x+1))\right))\\\\=\boxed{(2x+1)/(4x^2)}`

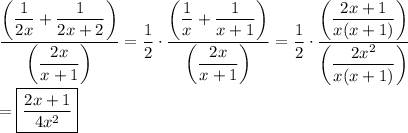
The expression is undefined for any denominator equal to zero: x=0 or x=-1.