Question

Help please❗❗❗❗❗❗❗❗❗❗❗❗

Valerie cut a piece of material to use as a pattern. She drew a sketch of the piece of material on the coordinate plane below.




If the length of each square represents one inch, what is the length from corner B to corner C?

A.

15 inches

B.

12 inches

C.

14 inches

D.

13 inches

Answer 1

Answer: C) 14 inches

===========================================================

Step-by-step explanation:

There are three methods to solve this problem

--------------------------

Method #1

Let point D be at the location (0,6). So this point is on line BC such that it cuts BC into two pieces of BD and DC.

BD is 7 inches long since it spans from x = -7 to x = 0

DC is also 7 inches long because it spans from x = 0 to x = 7

We can treat everything on line BC as if it was a number line.

So overall, BC = BD+DC = 7+7 = 14 inches

--------------------------

Method #2

Because points B and C are on the same horizontal level, we can subtract the x coordinates of each point. We apply absolute value to ensure the result of subtraction is never negative.

|B-C| = |-7-7| = |-14| = 14

or

|C - B| = |7 - (-7)| = |7 + 7| = |14| = 14

The order of subtraction doesn't matter as long as you use absolute value.

----------------------------

Method #3

We can use the distance formula to compute the distance from B(-7,6) to C(7,6)

So we'll make (x1,y1) = (-7,6) and (x2,y2) = (7,6)

Then we have the following steps

`d = \text{Distance from B to C}\\\\d = √((x_1 - x_2)^2 + (y_1 - y_2)^2)\\\\d = √((-7-7)^2 + (6-6)^2)\\\\d = √((-14)^2 + (0)^2)\\\\d = √(196 + 0)\\\\d = √(196)\\\\d = 14\\\\`

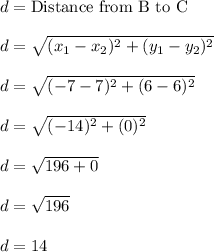
The distance from B to C is 14 inches, which is the same as saying segment BC is 14 inches long.

The distance formula is overkill in my opinion, so method 1 or 2 might be the better option.