Answer:
The area of the triangle is 84.511 square units.
Explanation:
First step, we need to calculate lengths of line segments AB, BC and AC by Pythagorean Theorem:
AB:
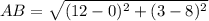
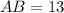
BC:

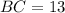
AC:
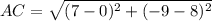
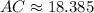
Now, we can determine the area of the triangle (
 ) by Heron's formula:
) by Heron's formula:
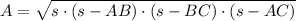 (1)
(1)
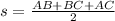 (2)
(2)
Where
 is the semiperimeter of the triangle.
is the semiperimeter of the triangle.
If we know that
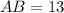 ,
,
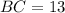 and
and
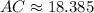 , then the area of the triangle is:
, then the area of the triangle is:
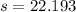

The area of the triangle is 84.511 square units.