Question

How can you use the formula for the volume of cylinder to remember the formula for the volume of a cone and the volume of a sphere?

Answer 1

The answer is a

Step-by-step explanation:

because the cone's volume is exactly one third ( 13 ) of a cylinder's volume and the sphere's volume is 43 vs 2 for the cylinder

Or more simply the sphere's volume is 23 of the cylinder's volume!

Answer 2

Answer: Choice A

The formula for the volume of a cone is 1/3 the volume of a cylinder. The volume of a sphere is 4/3 the volume of a cylinder, where the height of the cylinder is the same as the radius of the sphere

==============================================================

Step-by-step explanation:

As the first screenshot shows, the volume of a cone is 1/3 the volume of a sphere. The radius of each are the same. The height of each are the same as well.

The first screenshot also mentions "The volume of the half sphere is 2/3 the volume of the cylinder". The diagram shows the height of the cylinder (h) is equal to the radius of the half sphere. Based on this, the volume of a full sphere of radius r will be 4/3 times the volume of the cylinder with the same radius and height of 2r. You can think of having a spherical tennis ball inside a cylindrical can.

The first screenshot shows this when your teacher computed
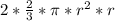`2*(2)/(3)*\pi*r^2*r` to get
`(4)/(3)\pi*r^3`

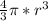
Note how
`(4)/(3)\pi*r^3 = (4)/(3)\left(\pi*r^2*r\right)`

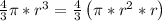
The stuff in parenthesis represents the volume of a cylinder with radius r and height h = r. This is one way to see that

SphereVolume = (4/3)*(CylinderVolume)

where the height of the cylinder is as discussed above.