9514 1404 393
Answer:
x = 4
Explanation:
I like to put these in the form f(x) = 0. We can do that by subtracting the right side. Common factors can be cancelled from numerator and denominator, provided they are not zero.
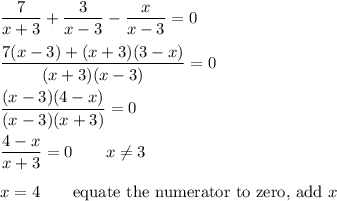
_____
If you leave the numerator as (x-3)(4-x), then there are two values of x that make it zero. Because x=3 makes the equation "undefined", it cannot be considered to be a solution.