Question

ALL YOU NEED IS IN THE PHOTO PLEASE DON'T DO STEP BY STEP PUT ONLY THE ANSWER PLEASEEEEEEEEEEEEEEEEEEEEE hhgfdfgg shrinks Zuniga​

Answer 1

Option (3)

Explanation:

Value of a car with a depreciation rate 'r' after time 't' is given by the formula,

v(t) =
`v_0(1-(r)/(100))^t`

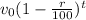
Here, v(t) = Final value

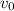`v_0` = Initial value

r = rate of depreciation

From the given function,

v(t) =
`24893(0.88)^t`

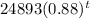
v(t) =
`24893(1-0.12)^t`

=
`24893(1-(12)/(100))^t`

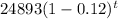
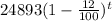
Now we compare this expression with the formula of depreciation.

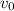`v_0` = 24893

r = 12%

Therefore, Option (3) will be the answer.