Answer:
The central angle is 5/3 radians or approximately 95.4930°.
Step-by-step explanation:
Recall that arc-length is given by the formula:
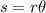
Where s is the arc-length, r is the radius of the circle, and θ is the measure of the central angle, in radians.
Since the intercepted arc-length is 10 meters and the radius is 6 meters:
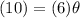
Solve for θ:

The central angle measures 5/3 radians.
Recall that to convert from radians to degrees, we can multiply by 180°/π. Hence:
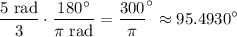
So, the central angle is approximately 95.4930°