The partial derivative
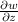 for the given function x^5w + w^7 + wz^2 + 8yz = 0 is
for the given function x^5w + w^7 + wz^2 + 8yz = 0 is
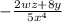 , obtained through the process of implicit differentiation.
, obtained through the process of implicit differentiation.
To find the partial derivative
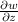 for the given implicit function
for the given implicit function
 , we'll use implicit differentiation.
, we'll use implicit differentiation.
Start by taking the partial derivative of each term with respect to z:
![\[5x^4 (\partial w)/(\partial z) + 2wz + 8y = 0.\]](https://img.qammunity.org/qa-images/2022/formulas/mathematics/college/121ago1sajsgthxpk6fe51.png)
Next, isolate
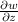 :
:
![\[5x^4 (\partial w)/(\partial z) = -2wz - 8y.\]](https://img.qammunity.org/qa-images/2022/formulas/mathematics/college/dy6lckt41t34n6m1urzrpa.png)
Now, solve for
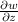 :
:
![\[(\partial w)/(\partial z) = -(2wz + 8y)/(5x^4).\]](https://img.qammunity.org/qa-images/2022/formulas/mathematics/college/ew9gtwo1wf25sob9vhx9p0.png)
This is the partial derivative of w with respect to z.
In conclusion, the partial derivative expresses the rate of change of w with respect to z in the context of the given implicit equation.