Question

Consider the quadratic function f(x)= 9x^2+30x+25=0

Part a: find a value of the discriminant for the function.

A) 3
B) 6
C) 25
D) 0

Answer 1

D) 0

There is 1 real solution.

Explanation:

Hi there!

`f(x)= 9x^2+30x+25=0`

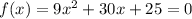
This is written in standard form:

`f(x)=ax^2+bx+c`

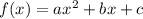
This means:

a=9

b=30

c=25

The discriminant states:

`D=b^2-4ac`

If D>0, there are 2 real solutions.

If D=0, there is 1 real solution.

If D<0, there are 2 complex solutions.

Plug in the values:

`D=30^2-4(9)(25)\\D=0`

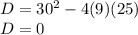
Therefore, there is 1 real solution.

I hope this helps!