Answer:
![y=(-1)/(2) \sqrt[]{4x^2+4c_(1)^2} -c_(1)\ or \ (1)/(2) \sqrt[]{4x^2+4c_(1)^2} -c_(1)](https://img.qammunity.org/2022/formulas/mathematics/college/fk1c83d5e8ocuvzekun8n7l75g9q4e12av.png)
Explanation:
As it is first order nonlinear ordinary differential equation
Let y(x) = x v(x)
2xy/(x²+y²)=2v/(v^2+1)
dy=xdv+vdx
dy/dx=d(dv/dx)+v
x(dv/dx)+v=(2v)/(v^2+1)
dv/dx=[(2v)/(v^2+1)-v]/x
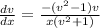
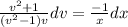
∫
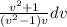 = ∫
= ∫
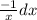
u=v^2
du=2vdv
Left hand side:
∫
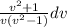
=∫

=
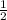 ∫
∫

=
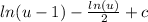
=
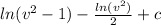
Right hand side:
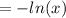
Solve for v:
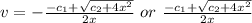
![y=(-1)/(2) \sqrt[]{4x^2+4c_(1)^2} -c_(1)\ or \ (1)/(2) \sqrt[]{4x^2+4c_(1)^2} -c_(1)](https://img.qammunity.org/2022/formulas/mathematics/college/fk1c83d5e8ocuvzekun8n7l75g9q4e12av.png)